We are given that the length of a rectangle is 3 inches greater than the width.
Let us draw a rectangle and label the width and length.
Part A:
Let the width of the rectangle is x inches.
Then the length of the rectangle is (x + 3) inches.
Now recall that the area of a rectangle is given by
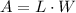
Where L is the length and W is the width of the rectangle.

Therefore, the above polynomial represents the area of the rectangle.
Part B:
We are given that the width is 4 inches.
Substitute the width (x = 4) into the equation of the area that we found in part A.
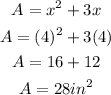
Therefore, the area of the rectangle is 28 square inches.