To graph this linear function, we can find both intercepts of the function. To achieve this, we need to solve the equation when y = 0 (for this function) (this will be the x-intercept), and then we need to solve the resulting equation for this function when x = 0 (this will be the y-intercept). Then, we will have two points for which we can graph the function - we need to remember that a line is defined by two points.
Then, we can proceed as follows:
1. Finding the x-intercept

Then, we have:
a. Add -9 to both sides of the equation:
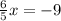
b. Multiply both sides of the equation by 5/6:

Therefore, the x-intercept is (-7.5, 0).
2. Finding the y-intercept
We have that x = 0 in this case. Then, we have:
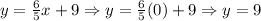
Therefore, the y-intercept is (0, 9).
Now, we have the points (-7.5, 0) and (0, 9), and we can draw both points on the coordinate plane. The line will pass through these two points: