To answer this question we need the equation of a parabola that uses the distance from the focus to the vertex.
This formula is,
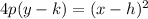
where,
p is the distance from the focus to the vertex, and the point (h,k) is the vertex.
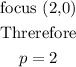
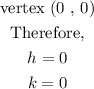
Let us now substitute the data into the equation of the parabola,
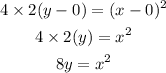
Hence, the equation for the parabola is, x² = 8y.
Option C is the correct answer.