Question

Find the equation for thefollowing parabola.Vertex (0,0)Focus (2, 0)A. 2x^2 = yB. y^2 = 8x2C. X^2 = ByD. y^2 = 8x

Answer 1

To answer this question we need the equation of a parabola that uses the distance from the focus to the vertex.

This formula is,

`4p(y-k)=(x-h)^2`

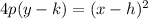
where,

p is the distance from the focus to the vertex, and the point (h,k) is the vertex.

`\begin{gathered} \text{focus (2,0)} \\ \text{Threrefore} \\ p=2 \end{gathered}`
`\begin{gathered} \text{vertex (0 , 0)} \\ \text{Therefore,} \\ h=0 \\ k=0 \end{gathered}`

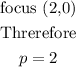
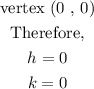
Let us now substitute the data into the equation of the parabola,

`\begin{gathered} 4*2(y-0)=(x-0)^2 \\ 4*2(y)=x^2 \\ 8y=x^2 \end{gathered}`

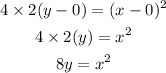
Hence, the equation for the parabola is, x² = 8y.

Option C is the correct answer.