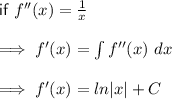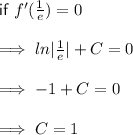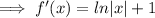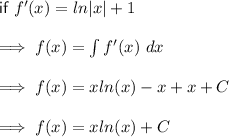Answer:
b) local minimum at

c) Graph of the function is convex
Explanation:
We are told that
 , which implies there is a turning/stationary point at
, which implies there is a turning/stationary point at
 .
.
Substituting
 into
into
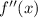 will tell us if the turning point is a minimum or a maximum:
will tell us if the turning point is a minimum or a maximum:
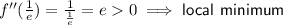
Therefore, statement a) is false and statement b) is true.
If the function has a minimum turning point, then this implies that the curve is convex. Therefore, statement c) is true.
Extremum = local min and max points.
We have already established that there is a local minimum at
 , therefore statement d) is false.
, therefore statement d) is false.
I know this is not needed for this question, but here are the workings to detemine the equation of the function (I've also attached a graph). This supports the answers above.