We have a sample that is:
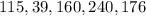
a) We can find the median by first sorting the sample:

The median is the value that has 50% of the values below its values.
In this case, this value is in the third place of the sorted sample and has a value of 160.
b) We have to find the mean.
We can calculate it as:
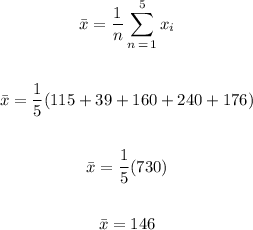
c) We have to calculate the variance. To find its value we will use the mean value we have just calculated:
![\begin{gathered} s^2=(1)/(n)\sum_{n\mathop{=}1}^5(x_i-\bar{x})^2 \\ \\ s^2=(1)/(5)[(115-146)^2+(39-146)^2+(160-146)^2+(240-146)^2+(176-146)^2] \\ \\ s^2=(1)/(5)[(-31)^2+(-107)^2+(14)^2+(94)^2+(30)^2] \\ \\ s^2=(1)/(5)(961+11449+196+8836+900) \\ \\ s^2=(1)/(5)(22342) \\ \\ s^2=4468.4 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/2b8msl89mn3vv4lij7t5wnyo8k4pu7btqx.png)
d) We have to calculate the standard deviation. As we have already calculated the variance, we can calculate it as:
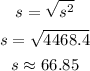
e) We now have to find the coefficient of variation:
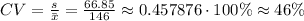
Answer:
a) 160
b) 146
c) 4468.4
d) 66.85
e) 46%