Question

What are the answers for a, b and c in MJ?

Answer 1

Given:

The orbital height of the satellite, h=94 km=94000 m

The mass of the satellite, m=1045 kg

The new altitude of the satellite, d=207 km=207000 m

To find:

a) The energy needed.

b) The change in the kinetic energy.

c) The change in the potential energy.

Step-by-step explanation:

The radius of the earth, R=6.37×10⁶ m

The mass of the earth, M=6×10²⁴ kg

a) The orbital velocity is given by,

`v=\sqrt{(GM)/(r)}`

Where G is the gravitational constant and r is the radius of the satellite from the center of the earth.

Thus the initial orbital velocity of the earth,

`\begin{gathered} v_1=\sqrt{(6.67*10^(-11)*6*10^(24))/((6.37×10^6+94000))} \\ =7868.43\text{ m/s} \end{gathered}`

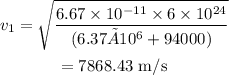
The orbital velocity after changing the altitude is,

`\begin{gathered} v_2=\sqrt{(6.67*10^(-11)*6*10^(24))/((6.37*10^6+207000))} \\ =7800.5\text{ m/s} \end{gathered}`

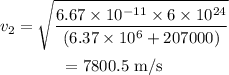
Thus the total energy needed is given by,

`E=((1)/(2)mv_2^2-(GMm)/((R+d)))-((1)/(2)mv_1^2-(GMm)/((R+h)))`

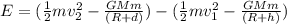
On substituting the known values,

`\begin{gathered} E=1045[((1)/(2)*7868.43^2-(6.67*10^(-11)*6*10^(24))/((6.37*10^6+207000)))-((1)/(2)*7800.5^2-(6.67*10^(-11)*6*10^(24))/((6.37×10^6+94000)))] \\ =623\text{ MJ} \end{gathered}`

b)

The change in the kinetic energy is given by,

`\begin{gathered} KE=(1)/(2)mv_2^2-(1)/(2)mv_1^2 \\ =(1)/(2)m(v_2^2-v_1^2) \end{gathered}`

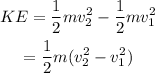
On substituting the known values,