Question

Finding a specify term of a geometric sequence given the common ratio and first term

Answer 1

Step-by-step explanation

A geometric sequence is defined as:

`\begin{gathered} a_1=a*r^0=a*r^(1-1), \\ a_2=a*r^1=a*r^(2-1), \\ a_3=a*r^2=a*r^(3-1), \\ ... \\ a_7=a*r^6=a*r^(7-1), \\ ... \end{gathered}`

Where r ≠ 0 is the common ratio and a ≠ 0 is the first term of the sequence.

From the statement, we know that r = 2/3 and the first term is a = 5.

Replacing these numbers in the expression of the 7th term, we get:

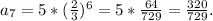`a_7=5*((2)/(3))^6=5*(64)/(729)=(320)/(729).`Answer

320/729