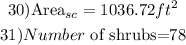
Step-by-step explanation
the area of a circular sector is given by
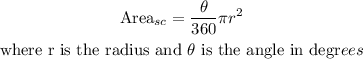
then
Step 1
Let
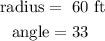
now, replace in the formula

Step 2
if shrubs are planted every 2 ft along the outer border of the garden, how many shrubs
are needed?
to figure out this, we need to take the perimeter of the circular sector and divide by 2 ft, to get the total number of shrubs in the border
so,
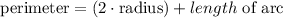
so, we need to find the length of the arc
the length of the arc is given by
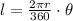
replace.
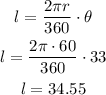
finally, replace in the perimeter formula
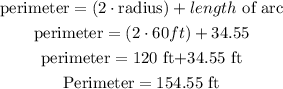
divde by 2 to know the numbers of shrubs
