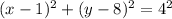The general equation of a circle is expressed as
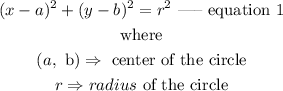
Given that a circle having equation
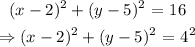
is moved up 3 units and 1 unit to the left. Thus, we have
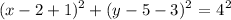
This gives
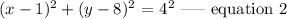
Comparing equations 1 and 2, we have
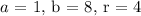
Hence,
the center (a, b) of the circle is (1, 8),
the radius r of the circle is 4,
the equation of the circle is