Question

The quadratic equation y= -16t^2 +4t+2 represents a moving objects trajectory where y is the objects height in feet above the ground after t seconds . At what time will the objects hit the ground ?

Answer 1

Since y is the object's height, it will be on the ground when y = 0. So let's do that:

`0=-16t^2+4t+2`

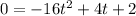
Here, we can use Bhaskara's Formula to find the roots of the equation:

`\begin{gathered} t=\frac{-4\pm\sqrt[]{4^2-4\cdot(-16)\cdot2}}{2\cdot(-16)} \\ t=\frac{-4\pm\sqrt[]{16+128}}{-32}=\frac{-4\pm\sqrt[]{144}}{-32}=(-4\pm12)/(-32) \\ t_1=(-4+12)/(-32)=(8)/(-32)=-0.25 \\ t_2=(-4-12)/(-32)=(-16)/(-32)=0.5 \end{gathered}`

Since the time at start is 0, we can't have a negative sign, it would be like saying what happened before the object was in the air. The it will hit the ground at t = 0.5 s.