It is given that there are two types of milk.
One is 3.5% and one is 0%.
Let the number of cups of 3.5% milk be x and the number of cups of 0% milk used be y.
The total should be 3 cups so it follows:
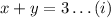
It is also known that the resulting milk is 2% so it follows:
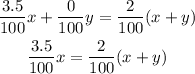
Multiply by 100 on both sides to get:
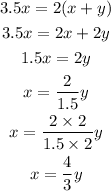
Substitute the value of (ii) in (i) to get:
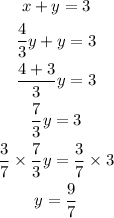
Hence the quantity of 0% milk is 9/7 cups.
The quantity of 3.5% milk is given by:
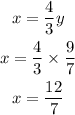
Hence the quantity of 3.5% milk is 12/7 cups.