Question

Create an equation that models the table below. Use the variables in the table for your equation. Write your equation with 'S' isolated.

Answer 1

The table show piszzas (P) on the left column and the slices of Pepperonin (S) on the right column.

To determine the equation models first check the ratio S/P to determine whether they are proportinal or not.

`\begin{gathered} (36)/(3)=12 \\ (96)/(8)=12 \\ (228)/(19)=12 \end{gathered}`

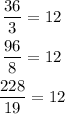
Now as the ratios are constant it mean the variation is linear and the relationship is proportional.

Thus the model equation can be determine as,

`\begin{gathered} (S)/(P)=12 \\ S=12P \end{gathered}`

Thus, the above equation gives the required model equation.