Question

A new born child receives a $8,000 gift toward a college education from her grandparents. How much will the $8,000 be worth in 17 years if it is invested at 72% compounded quarterly?It will be worth $(Round to the nearest cent)

Answer 1

Answer:

The money will be worth $618111016.19 at the end of 17 years

Step-by-step explanation:

Initial amount received, P = $3000

Interest rate, r = 72%

r = 72/100

r = 0.72

Number of times compounded in a year, n = 4

Time, t = 17 years

Amount after 17 years will be calculated as:

`A=P(1+(r)/(n))^(nt)`

Substitute P = 8000, r = 0.72, n = 4, and t = 17 into the formula above

`A=8000(1+(0.72)/(4))^(4(17))`
`\begin{gathered} A=8000(1+0.18)^(68) \\ A=8000(1.18)^(68) \end{gathered}`

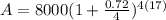
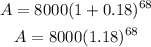
A = $618111016.19

The money will be worth $618111016.19 at the end of 17 years