Question

You deposit $5000 in an account earning 6% interest compounded continuously. How much will you have in the account in 5 years?

Answer 1

For us to determine how much the account will be in 5 years at compounded continuously, we will be using the following formula:

`\text{ A = P}_0e^(rt)`

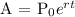
Where,

P = Principal amount (Initial Value)

A = Final amount (Future Value)

r = interest rate (in decimal)

t = time (in years)

e = mathematical constant approximately 2.7183

Given:

P = $5,000

r = 6% = 6/100 = 0.06

t = 5 years

We get,

`\text{ A = P}_0e^(rt)`
`\text{ A = (5,000)(2.7183)}^((0.06)(5))`
`\text{ A = (5,000)(2.7183)}^(0.3)`
`\text{ A = (5,000)(}1.34986151469)`
`\text{ A = }6,749.30757343\text{ }\approx\text{ \$6,749.30}`

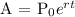
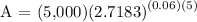
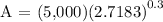
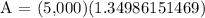
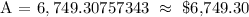
Therefore, in 5 years, at 6% compounded continuously, your account will be $6,749.30