Question

Find the solutions of the given system of equations: x2 + y2 = 68 and y = 4x.

Answer 1

Given the system of equations:

`\begin{gathered} x^2+y^2=68 \\ y=4x \end{gathered}`

We can solve it by substituting the second equation into the first as follows:

`\begin{gathered} x^2+(4x)^2=68 \\ \\ Operating: \\ \\ x^2+16x^2=68 \\ 17x^2=68 \end{gathered}`

Dividing by 17:

`x^2=(68)/(17)=4`

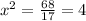
Applying square root on both sides:

`\begin{gathered} x=\pm√(4) \\ x=\pm2 \end{gathered}`

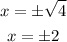
There are two solutions for x and they produce two solutions for y.

For x = 2

y = 4*2 = 8

For x = -2

y = 4*(-2) = -8

Thus, the solutions are:

(2,8) and (-2, -8)