1 Answer

Satria Suria · Answer 1 · 2023-03-18T23:22:58+0000

Question: what are the factors of the expression:

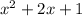
Solution:

Let the expression

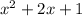
If we apply the quadratic equation:

$\frac{-b\pm\sqrt[]{b^2-4ac}}{2a}$

we get the zero of the polynomial

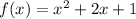
which is -1. Thus the polynomial can be factored in the following way

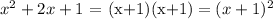
$x^2+2x+1\text{ = (x+1)(x+1)}=(x+1)^2$

then, we can conclude that the factors of the given polynomial are:

(x+1) and (x+1)

Please log in or register to add a comment.