Question

Determine the required value of a missing probability to make the distribution a discrete probability distribution… p(4) =

Answer 1

The table given showed the discrete probability distribution for random variables 3 to 6 and their corresponding probability except for the probability of 4

It should be noted that for a probability distribution, the cummulative probabibility (that is the sum of all the probability) must be equal to one.

This means that

`P(3)+P(4)+P(5)+P(6)=1`

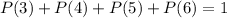
From the given table, it can be seen that

`\begin{gathered} P(3)=0.32 \\ P(4)=\text{?} \\ P(5)=0.17 \\ P(6)=0.26 \end{gathered}`

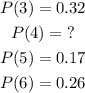
Then, p(4) is calculated below

`\begin{gathered} P(3)+P(4)+P(5)+P(6)=1 \\ 0.32+P(4)+0.17+0.26=1 \\ P(4)+0.32+0.17+0.26=1_{} \\ P(4)+0.75=1 \\ P(4)=1-0.75 \\ P(4)=0.25 \end{gathered}`

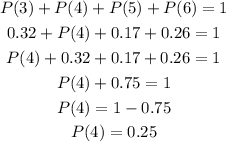
Hence, P(4) is 0.25