Question

1c. Clue 1The number has three digits.Clue 2 The number is less than 140.Clue 3 The number has 7 as a factor.Clue 4 The number is even.Clue 5 The sum of the digits of the number is less than 9.

Answer 1

We have an even 3 digits number whose sum lie is less than 9, has got 3 digits and less than 140.

We will establish the inequalities that satisfies the conditions given and then figure out the number.

`\begin{gathered} 100x+10y+z<140 \\ x+y+z<9 \\ 100x+10y+z=14a\text{ where a lies between 8 and 9} \end{gathered}`

From our last inequality, we can easily see that the number in question is 14 x 8 or 14 x 9. Any multiple of 7 that is even is also a multiple of 14.

`\begin{gathered} 14*8=112\text{ AND} \\ 14*9=126 \end{gathered}`

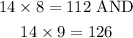
From the above, it can be easily seen that 112 satisfies the conditions listed.

The number is 112