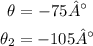Question

2. State two (2) values of θ (theta) to the nearest degree forsin θ = − 0. 966

Answer 1

To find a value of θ theta given a value of sin(θ) we must use the arcsin function, it receives a value of an sin as argument and returns the value of the angle θ. Then we must use a calculator and input

`\begin{gathered} \theta=\arcsin\left(x\right) \\ \\ \theta=\arcsin(-0.966) \\ \\ \theta=−75 \end{gathered}`

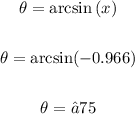
The result is already rounded to the nearest degree. Therefore, one value of θ that satisfies sin θ = −0.966 is θ= -75°

Now to find the other value we will look at the symmetry in the trigonometric circle:

Then, the other value of theta will be

`\begin{gathered} \theta_2=-75°-30° \\ \\ \theta_2=105° \end{gathered}`

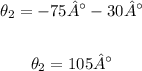
Final answer:

`\begin{gathered} \theta=-75° \\ \theta_2=-105° \end{gathered}`