First, we need to find the sides of the triangle.
The base of the triangles is 8ft - 5ft = 3ft.
The height for the triangle is 7ft - 4ft = 3ft
Now, we need to find the area of the triangle:
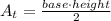
Replacing the values:
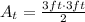
Then
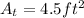
Now, we need to find the area for the rectangle:
Area for a rectangle = Length * Width
In this case:
Length = 8ft
Width = 7ft
Therefore:
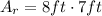
Then
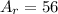
Finally, to find the area of the shaded region we need to subtract the triangle area from the rectangle area:
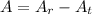
Therefore:
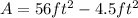
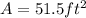
Hence, the area for the shaded region is 51.5 ft².