Question

Use Polya's four-step problem-solving strategy and the problem-solving procedures presented in this section to solve the following exercise.A shirt and a tie together cost $68. The shirt costs $30 more than the tie. What is the cost of the shirt (in dollars).

Answer 1

Let x and y be the cost of a shirt and a tie, respectively; therefore, the two equations are

`\begin{gathered} x+y=68 \\ \text{and} \\ x=30+y \end{gathered}`

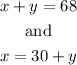
We have two variables and two equations; we need to solve the system of equations to find the values of x and y.

Solve using the substitution method.

Use the second equation into the first equation, as shown below

`\begin{gathered} x=30+y \\ \Rightarrow(30+y)+y=68 \\ \Rightarrow30+2y=68 \\ \Rightarrow2y=68-30=38 \\ \Rightarrow y=(38)/(2) \\ \Rightarrow y=19 \end{gathered}`

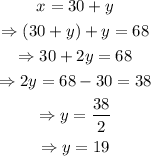
Now, use this value of y in the second equation

`\begin{gathered} y=19 \\ \Rightarrow x=30+y=30+19 \\ \Rightarrow x=49 \end{gathered}`

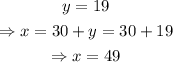
Remember that x is the cost of a shirt and y is the cost of a tie. Therefore, the answers are

Cost of a shirt: $49

Cost of a tie: $19

One can verify the answer by noticing that a shirt and a tie cost $49+$19=$68, and that a shirt costs $30+$19=$49