Let 1 and 2 mean that a person is right-handed or left-handed, respectively.
Consider the probability space as the different groups of 12 people that can be formed with the 29 total people. {(1,1,1,1,1,...1),(2,1,1,1,1,...,1),...}
We need to use the binomial distribution in order to find the answer.
Consider X to be the number of right-handed people in the group.
The probability of X=3 is then:
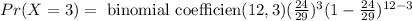
We used the formula

Finally, we need to simplify the expression, as shown below
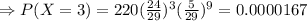
This is the answer one obtains using the binomial distribution; nevertheless, the actual probability is equal to zero because it is not possible to form a group of 12 people that only contains 3 right-handed people as there are only 5 left-handed people (3+5=8).