Question

2. Using Vièta's theorem, find the solutions to the equation. a) x^2 - 3x + 2 = 0 b) x^2 + 2x - 15 = 0.

Answer 1

Given:

`\begin{gathered} x^2-3x+2=0 \\ x^2+2x-15=0 \end{gathered}`

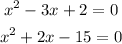
Required:

We need to find the solution by Vièta's theorem.

Step-by-step explanation:

Compare 1st equation with

`ax^2+bx+c=0`

we get

`\begin{gathered} a=1 \\ b=-3 \\ c=2 \end{gathered}`

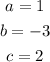
Vièta's theorem is

`\begin{gathered} x_1+x_2=-(b)/(a) \\ x_1x_2=(c)/(a) \end{gathered}`

`\begin{gathered} x_1+x_2=3 \\ x_1x_2=2 \end{gathered}`

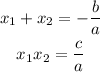
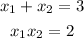
now solve this equation and we get

`\begin{gathered} x_1=1 \\ x_2=2 \end{gathered}`

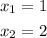
because addition of 1 and 2 is 3 and multiplication is 2

Now for 2nd equation

`\begin{gathered} a=1 \\ b=2 \\ c=-15 \end{gathered}`

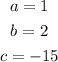
apply Vièta's theorem

`\begin{gathered} x_1+x_2=-2 \\ x_1x_2=-15 \end{gathered}`

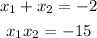
by this

`\begin{gathered} x_1=3 \\ x_2=-5 \end{gathered}`

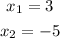
because addition of 3 and -5 is -2 and multiplication is -15