Question

a large human population of both globally and within individual countries has been a concern since the time of Thomas Malthus. country X is 95% desert. the government of country X is concerned about not having enough arable land (land capable of being used to grow crops) in the country to produce the food needed to feed its population without increasing food imports the demographic for Country X for the year 2020 is provided in the table below. 1. calculate the national population growth rate for a country X 2. using the rule of 70 calculate the doubling time for this population

Answer 1

`\begin{gathered} \text{National population growth rate is }(12)/(1000) \\ \\ \text{Doubling time is 5833 years and 4 months} \end{gathered}`

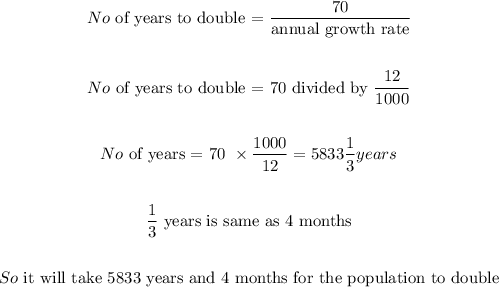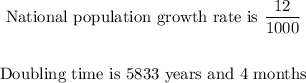
Firstly, we want to calculate the growth rate of the population

While birth would increase the population, death and migration will decrease the population

So when we subtract the migration rate and the death rate from the birth rate, we can get the population growth rate;

Thus, we have;

`\begin{gathered} (38)/(1000)\text{ - (}(24)/(1000)\text{ + }(2)/(1000)) \\ \\ =\text{ }(38)/(1000)\text{ - }(26)/(1000) \\ \\ =\text{ }(12)/(1000) \end{gathered}`

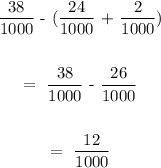
The national population growth rate for a country X is 12/1000

Secondly, we are to use the rule of 70 to calculate the doubling time for the population

Mathematically;

`\begin{gathered} No\text{ of years to double = }\frac{70}{\text{annual growth rate}} \\ \\ No\text{ of years to double = 70 divided by }(12)/(1000) \\ \\ No\text{ of years = 70 }*(1000)/(12)=5833(1)/(3)years^{} \\ \\ (1)/(3)\text{ years is same as 4 months} \\ \\ So\text{ it will take 5833 years and 4 months for the population to double} \end{gathered}`