In this problem the function that models the hight is:

So when the water hits the grownd h=0 so we replace that and solve for t so:
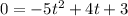
To solve this expression we can use the cuadratic equation:
![x=\frac{-4\pm\sqrt[]{16-4(-5)(3)}}{-10}](https://img.qammunity.org/2023/formulas/mathematics/high-school/ho4leo7x10qf9xfb61889rsogszhdpsoxk.png)
and we operate so:
![\begin{gathered} x=\frac{-4\pm\sqrt[]{76}}{-10} \\ x=(-4\pm8.7)/(-10) \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/high-school/f5crpcjg2mp9ct9zq17eeigvbkz9ggbqzf.png)
Now we solve bout of the equation so:
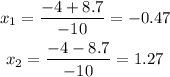
So the answer that have sense is the secon one so the water hits the ground after 1.27 seconds