We need to identify the team that has the smallest sample standard deviation.
In order to do so, we need to find the stand deviation of each experiment based on the confidence level and confidence interval of each of them.
A. A confidence level of 99.7% corresponds to a confidence interval of 3 standard deviations above and 3 standard deviations below the mean.
Thus, for the confidence interval 42 to 48, the mean is 45. And the standard deviation is given by:
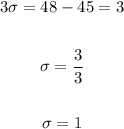
B. A confidence level of 95% corresponds to a confident interval of 2 standard deviations above and 2 standard deviations below the mean.
Thus, for the confidence interval 43 to 47, the mean is 45. And the standard deviation is given by:
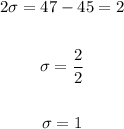
C. A confidence level of 68% corresponds to a confident interval of 1 standard deviation above and 1 standard deviation below the mean.
Thus, for the confidence interval 44 to 46, the mean is 45. And the standard deviation is given by:
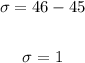
D. Again, we have a confidence level of 95%, which corresponds to 2 standard deviations.
Thus, for the confidence interval 44 to 46, the mean is 45. And the standard deviation is given by:

Therefore, the team that has the smallest sample standard deviation is:
Answer