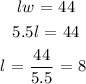Question

O EQUATIONS AND INEQUALITIESSolving a word problem using a quadratic equation with rationa...

Answer 1

`\begin{gathered} length\text{ = 8 m} \\ width\text{ = 5.5 m} \end{gathered}`

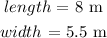
Step-by-step explanation:

Here, we want to get the dimensions of the rectangle

Let us represent the length by l and the width by w

From the question:

The length of the rectangle is 3 m less than double the width

Mathematically:

`l\text{ = 2w-3}`

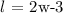
The product of the two represents the area

`\begin{gathered} A\text{ = l }*\text{ w} \\ lw\text{ = 44} \end{gathered}`

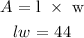
Now, let us substitute the first equation with the second:

`\begin{gathered} w(2w-3)\text{ = 44} \\ 2w^2-3w\text{ = 44} \\ 2w^2-3w-44\text{ = 0} \end{gathered}`

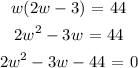
Solving the quadratic equation, we have:

`\begin{gathered} 2w^2-11w+8w-44\text{ = 0} \\ 2w^2+8w-11w-44\text{ = 0} \\ 2w(w\text{ + 4\rparen -11\lparen w+4\rparen = 0} \\ (2w-11)(w+4)\text{ = 0} \\ 2w=\text{ 11} \\ w\text{ = }(11)/(2) \\ \\ w\text{ = 5.5} \end{gathered}`

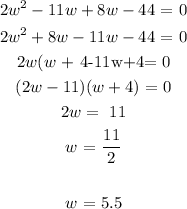
Recall:

`\begin{gathered} lw\text{ = 44} \\ 5.5l\text{ = 44} \\ l\text{ = }(44)/(5.5)\text{ = 8 } \end{gathered}`