Answer:
1) 29.82 cm
2) 5.76 cm
3) 35.58 cm
Step-by-step explanation:
Part 1)
The force of a spring is equal to:
F = kΔx
Where k is the constant of the spring and Δx is the elongation. Δx = xf - xi, where xf is the length of the spring when the force is applied and xi is the empty length. Then
F = k(xf - xi)
Now, by the action of a force of 51N, a spring measures 39 cm, so
51 = k(39 - xi)
And by the action of a force of 61N, the spring length is 40.8 cm, so
61 = k(40.8 - xi)
To find the empty length, we need to solve the system of equations
51 = k(39 - xi)
61 = k(40.8 - xi)
First, solve the first equation for k
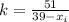
Then, replace this on the second equation and solve for xi
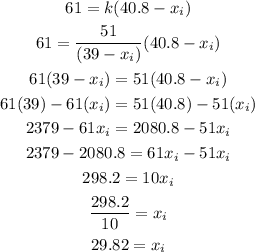
Therefore, the empty length of the spring is 29.82 cm
Part 2)
Now, we need to calculate the value of k, so replacing xi = 29.82, we get:
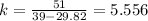
Therefore, the equation for the force is
F = 5.556Δx
Solving for Δx, we get:
Δx = F/5.556
Replacing the force by 32N, we can calculate the elongation as
Δx = 32/5.556 = 5.76 cm
Part 3)
Then, the length can be calculated by solving the following equation for xf
Δx = xf - xi
xf = Δx + xi
Replacing Δx = 5.76 cm and xi = 29.82 cm, we get:
xf = 5.76 cm + 29.82 cm
xf = 35.58 cm
So, its length is 35.58 cm
Therefore, the answers are
1) 29.82 cm
2) 5.76 cm
3) 35.58 cm