Question

20 P1: a For two events, A and B.P(B) -0.5, P(AB) -0.4 andPAB) = 0.4.Calculatei PAB)ii P(A)ili P(AUB)iv P(AB)(8 marks)b Determine, with a reason, whetherevents A and B are independent ornot.(2 marks)probabilityStatistics and

Answer 1

We have two events A and B.

We know that:

P(B) = 0.5

P(A|B) = 0.4

P(A∩B') = 0.4

i) We have to calculate P(A∩B).

We can relate P(A∩B) with the other probabilities knowing that:

`(A\cap B)\cup(A\cap B^(\prime))=A`

So we can write:

`P(A\cap B)+P(A\cap B^(\prime))=P(A)`

We know P(A∩B') but we don't know P(A), so this approach is not useful in this case.

We can try with the conditional probability relating P(A∩B) as:

`P(A|B)=(P(A\cap B))/(P(B))`

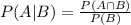
In this case, we can use this to calculate P(A∩B) as:

`\begin{gathered} P(A\cap B)=P(A|B)P(B) \\ P(A\cap B)=0.4*0.5 \\ P(A\cap B)=0.2 \end{gathered}`

ii) We have to calculate P(A) now.

We can use the first equation we derive to calculate it:

`\begin{gathered} P(A)=P(A\cap B)+P(A\cap B^(\prime)) \\ P(A)=0.2+0.4 \\ P(A)=0.6 \end{gathered}`

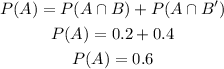
iii) We have to calculate P(A∪B).

We can use the expression:

`\begin{gathered} P(A\cup B)=P(A)+P(B)-P(A\cap B) \\ P(A\cup B)=0.6+0.4-0.2 \\ P(A\cup B)=0.8 \end{gathered}`

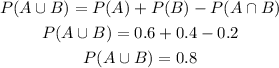
iv. We can now calculate P(A|B') as:

`\begin{gathered} P(A)=P(A|B)+P(A|B^(\prime)) \\ P(A|B^(\prime))=P(A)-P(A|B) \\ P(A|B^(\prime))=0.6-0.4 \\ P(A|B^(\prime))=0.2 \end{gathered}`

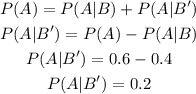
b) We now have to find if A and B are independent events.

To do that we have to verify this conditions:

`\begin{gathered} 1)P(A|B)=P(A) \\ 2)P(B|A)=P(B) \\ 3)P(A\cap B)=P(A)*P(B) \end{gathered}`

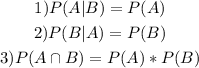
We can check for the first condition, as we already know the value:

`\begin{gathered} P(A|B)=0.4 \\ P(A)=0.6 \\ =>P(A|B)P(A) \end{gathered}`

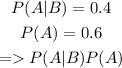
Then, the events are not independent.

Answer:

i) P(A∩B) = 0.2

ii) P(A) = 0.6

iii) P(A∪B) = 0.8

iv) P(A|B') = 0.2

b) The events are not independent.