The inverse of a matrix can be calculated as:
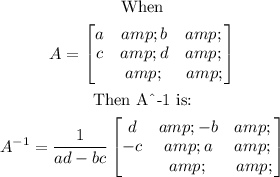
Then, let's start by calculating the inverse of the given matrix:
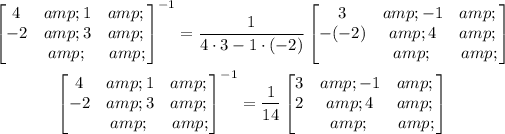
The problem says he multiplies the left side of the coefficient matrix by the inverse matrix, thus:
![\begin{gathered} \begin{bmatrix}{4} & {1} & {} \\ {-2} & {3} & {} \\ {} & {} & \end{bmatrix}^(-1)\begin{bmatrix}{4} & {1} & {} \\ {-2} & {3} & {} \\ {} & {} & \end{bmatrix}\cdot\begin{bmatrix}{x} & {} & {} \\ {y} & {} & {} \\ {} & {} & {}\end{bmatrix}=\begin{bmatrix}{4} & {1} & {} \\ {-2} & {3} & {} \\ {} & {} & \end{bmatrix}^(-1)\begin{bmatrix}{2} & {} & {} \\ {-22} & {} & {} \\ {} & {} & {}\end{bmatrix} \\ \end{gathered}]()
*These matrices will be the options to put on the first and second boxes.
Then:
![\begin{gathered} \begin{bmatrix}{x} & {} & {} \\ {y} & {} & {} \\ {} & {} & {}\end{bmatrix}=(1)/(14)\begin{bmatrix}{3} & -{1} & {} \\ {2} & {4} & {} \\ {} & {} & \end{bmatrix}\cdot\begin{bmatrix}{2} & {} & {} \\ {-22} & {} & {} \\ {} & {} & {}\end{bmatrix}\text{ This is for the third box} \\ \begin{bmatrix}{x} & {} & {} \\ {y} & {} & {} \\ {} & {} & {}\end{bmatrix}=(1)/(14)\begin{bmatrix}{3*2+(-1)*(-22)} & & {} \\ {2*2+4*(-22)} & & {} \\ {} & {} & \end{bmatrix}=(1)/(14)\begin{bmatrix}{28} & & {} \\ {-84} & & {} \\ {} & {} & \end{bmatrix}\text{ This is the 4th box} \\ \begin{bmatrix}{x} & {} & {} \\ {y} & {} & {} \\ {} & {} & {}\end{bmatrix}=\begin{bmatrix}{28/14} & & {} \\ {-84/14} & & {} \\ {} & {} & \end{bmatrix}=\begin{bmatrix}{2} & & {} \\ {-6} & & {} \\ {} & {} & \end{bmatrix}\text{ And finally this is the last box} \end{gathered}]()