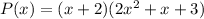Question

What is P(x) = 2x^3 + 5x^2 + 5x + 6 as a product of two factors.

Answer 1

So we have to write the following polynomial expression as a product of two factors:

`P(x)=2x^3+5x^2+5x+6`

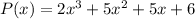
In order to do this we should find one of its roots first i.e. a x value that makes P(x)=0. If we use r to label this root we can write P like:

`P(x)=(x-r)\cdot(ax^2+bx+c)`

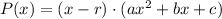
Where a, b and c are numbers that we can find using Ruffini's rule. So first of all let's find a root. We can use the rational root theorem. It states that if P(x) has rational roots then they are given by the quotient between a factor of the constant term (i.e. the number not multplied by powers of x) and a factor of the leading coefficient (i.e. the number multiplying the biggest power of x). In this case we have to look for the factors of 6 and 2 respectively. Their factors are:

`\begin{gathered} 6\colon6,-6,3,-3,2,-2,1,-1 \\ 2\colon2,-2,1,-1 \end{gathered}`

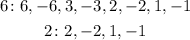
And the quotients and possible values for r are:

`6,-6,3,-3,2,-2,(3)/(2),-(3)/(2),1,-1,(1)/(2),-(1)/(2)`

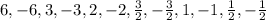
So one of these numbers make P(x) equal to zero. For example if we take x=-2 we get:

`\begin{gathered} P(-2)=2\cdot(-2)^3+5\cdot(-2)^2+5\cdot(-2)+6 \\ P(-2)=-16+20-10+6=0 \end{gathered}`

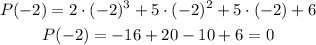
So -2 is a root of P(x) which means that we can take r=-2.

Now we can use Ruffini's law. On the first row we write the coefficients of P(x). Then the first one is repeated in the third row:

Now we multiply 2 by -2 and we write the result under the second coefficient. Then we add them:

Now we do the same with the 1:

And then we multiply 3 and -2 and add the result ot the last coefficient:

The numbers 2, 1 and 3 are the values of a,b and c respectively. Then we can write P(x) as a product of two factors and the answer is:

`P(x)=(x+2)(2x^2+x+3)`