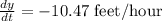Question

Yea I think and her dad is doing great so

Answer 1

Given the following function:

`tan\text{ }\theta=(10)/(y)`

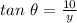
Both θ and y are functions of the time (t)

We will find the derivatives of θ and y with respect of the time (t) as follows:

`sec^2θ*(dθ)/(dt)=-(10)/(y^2)*(dy)/(dt)`

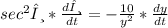
Now, we will find dy/dt when θ = π/6 and dθ/dt = π/12

First, we need to find the value of y when θ = π/6

`\begin{gathered} tan((\pi)/(6))=(10)/(y) \\ (1)/(√(3))=(10)/(y) \\ \\ y=10√(3) \end{gathered}`

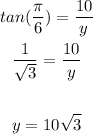
so, we will substitute the values to find dy/dt as follows:

`\begin{gathered} sec^2((\pi)/(6))*(\pi)/(12)=-(10)/((10√(3))^2)*(dy)/(dt) \\ \\ so,(dy)/(dt)=-((10√(3))^2)/(10)*sec^2((\pi)/(6))*(\pi)/(12)=-10.4719755 \end{gathered}`

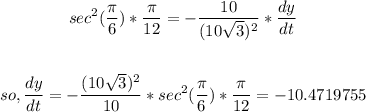
Rounding to 2 decimal places

So, the answer will be:

`(dy)/(dt)=-10.47\text{ feet/hour}`