Question

Find the 11th term of the arithmetic sequence -5x- 1, -8x + 4, -11 x+ 9, ...

Answer 1

Recall that an arithmetic sequence is a sequence in which the next term is obtained by adding a constant term to the previous one. Let us consider a1 = -5x-1 as the first term and let d be the constant term that is added to get the next term of the sequence. Using this, we get that

`a_2=a_1+d`

so if we replace the values, we get that

`-8x+4=-5x-1+d`

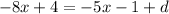
so, by adding 5x+1 on both sides, we get

`d=-8x+4+5x+1\text{ =(-8+5)x+5=-3x+5}`

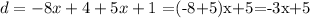
To check if this value of d is correct, lets add d to a2. We should get a3.

Note that

`a_2+d=-8x+4+(-3x+5)=-11x+9=a_3`

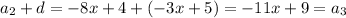
so the value of d is indeed correct.

Now, note the following

`a_3=a_2+d=(a_1+d)+d=a_1+2d=a_1+d\cdot(3-1)`

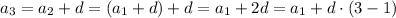
This suggest the following formula

`a_n=a_1+d\cdot(n-1)`

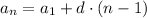
the question is asking for the 11th term of the sequence, that is, to replace the value of n=11 in this equation, so we get

`a_(11)=a_1+d\cdot(10)=-5x-1+10\cdot(-3x+5)\text{ =-5x-1-30x+50 = -35x+49}`

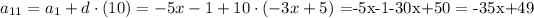
so the 11th term of the sequence is -35x+49