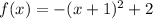Question

Write a formula for the function in the image below.

Answer 1

The vertex form of a quadratic function is:

`f(x)=a(x-h)^2+k`

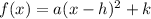
Where (h, k) is the vertex. Looking at the graph, the vertex is at (-1, 2), then:

`\begin{gathered} h=-1 \\ k=2 \\ \Rightarrow f(x)=a(x+1)^2+2 \end{gathered}`

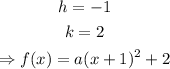
Finally, to find "a" we use the fact that 1 is the y-intercept of the graph (where the function is evaluated at x = 0). Then:

`\begin{gathered} f(0)=1\Rightarrow a(0+1)^2+2=1 \\ a=1-2 \\ \Rightarrow a=-1 \end{gathered}`

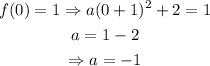
The final form of the function is:

`f(x)=-(x+1)^2+2`