Question

Josslyn placed $4,400 in a savings account which earns 3.2% interest, compounded annually. How much will she have in the account after 12 years?Round your answer to the nearest dollar.

Answer 1

The equation for the total amount after compounded interest is as follows:

`A=P(1+(r)/(n))^(nt)^{}`

Where A is the final amount, P is the initial amount, r is the annual interest, n is how many times per year the interest is compounded and t is the time in years.

Since the interest is compounded annually, it is compounded only once per year, so

`n=1`

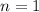
The other values are:

`\begin{gathered} P=4400 \\ r=3.2\%=0.032 \\ t=12 \end{gathered}`

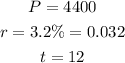
So, substituteing these into the equation, we have:

`\begin{gathered} A=4400(1+(0.032)/(1))^(1\cdot12) \\ A=4400(1+0.032)^(12) \\ A=4400(1.032)^(12) \\ A=4400\cdot1.4593\ldots \\ A=6421.0942\ldots\approx6421 \end{gathered}`

So, she will have approximately $6421.