Question

given circle K with diameter IJ and radius KG. GH is tangent to K at G. If GH =6 and KH =8, solve dor KG. Round your answer to the nearest tenth if necessary. If the answer cannot be determined click cannot be determined.

Answer 1

Step-by-step explanation:

We are given a circle K with radius KG. Note here that line KJ and line KG are both radii of the circle given.

Also we know that a line tangent to a circle at the point of intersecting with the radius forms a 90-degree angle with the radius.

We can now extract the following triangle from the diagram provided;

We now have a right triangle which we shall solve by use of the Pythagorean theorem;

`a^2+b^2=c^2`

Where we have c as the longest side (hypotenuse) and then a and b are the two other sides. Substituting into the equation above now gives us;

`\begin{gathered} a^2+b^2=c^2 \\ KG^2+6^2=8^2 \\ KG^2+36=64 \end{gathered}`

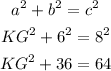
Subtract 36 from both sides;

`\begin{gathered} KG^2+36-36=64-36 \\ KG^2=28 \end{gathered}`

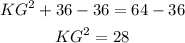
Take the square root of both sides;

`\begin{gathered} \sqrt[]{KG^2}=\sqrt[]{28} \\ KG=5.2915 \end{gathered}`

Rounded to the nearest tenth, the answer is;

ANSWER:

`KG=5.3`