Question

Reduce the rational expression to lowest terms. If it is already in lowest terms, enter the expression in the answerbox. Also, specify any restrictions on the variable.a²-3a-4/a² + 5a + 4Rational expression in lowest terms:Variable restrictions for the original expression: a

Answer 1

Factorize both quadratic polynomials, as shown below

`\begin{gathered} a^2-3a-4=0 \\ \Rightarrow a=(3\pm√(9+16))/(2)=(3\pm√(25))/(2)=(3\pm5)/(2)\Rightarrow a=-1,4 \\ \Rightarrow a^2-3a-4=(a+1)(a-4) \\ \end{gathered}`

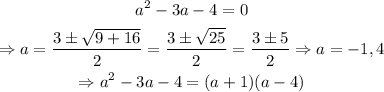
Similarly,

`\begin{gathered} a^2+5a+4=0 \\ \Rightarrow a=(-5\pm√(25-16))/(2)=(-5\pm3)/(2)\Rightarrow a=-1,-4 \\ \Rightarrow a^2+5a+4=(a+1)(a+4) \end{gathered}`

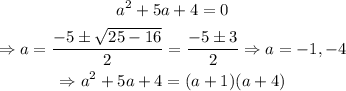
Thus,

`\Rightarrow(a^2-3a-4)/(a^2+5a+4)=((a+1)(a-4))/((a+1)(a+4))`

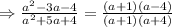
Therefore, since the denominator cannot be equal to zero.

The variable restrictions for the original expression are a≠-1,-4

Then, provided that a is different than -1,

`\Rightarrow(a^2-3a-4)/(a^2+5a+4)=(x-4)/(x+4)`

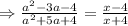
The rational expression in the lowest terms is (x-4)/(x+4)