Question

Identify point in region of inequalities

Answer 1

We want to picture the inequalities

`y<\text{ - x -3}`

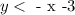
and

`y>(4)/(5)x\text{ +5}`

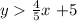
First, we consider the lines y= -x -3 and and y=(4/5) x +5 . Since the first line has a negative slope, this means that its graph should go downwards as x increases and since the other line has a positive slope, this means that its graph should go upwards as x increases. This leads to the following picture

Now, the expression

`y<\text{ -x -3}`

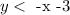
means that the y coordinate of the line should be below the red line. Also, the expression

`y>(4)/(5)x+5`

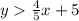
means tha the y coordinate should be above the blue line. If we combine both conditions, we find the following region

so we should look for a point that lies in this region

We are given the points (-1,9), (-6,2), (9,-9) and (-8,-5).

We see that the yellow region is located where the x coordinate is always negative. So, this means that we discard (9,-9).

so we should test the other points. Since -8 is the furthest to the left, let us calculate the value of each line at x=-8.

`\text{ -(-8) -3 = 8 -3 = 5}`

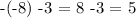
so, in this case the first expression is accomplished since -5 < 5. And

`(4)/(5)\cdot(\text{ -8)+5= =}\frac{\text{ -7}}{5}=\text{ -1.4}`

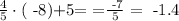
However note that -5 < 1.4, and it should be greater than -1.4 to be in the yellow region. So we discard the point (-8,-5) .

We can check , iusing the graph, that the lines cross at the point (-40/9, 13/9) which is about (-4.44, 1.44). This means that for the point to be on the yellow region, it should be on the left of -4.44. Since the only point that we are given that fulfills this condition is (-6, 2), this should be our answer. We check that

`\text{ -(-6)-3=3>2}`

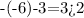
and

`(4)/(5)\cdot(\text{ -6)+5 = }(1)/(5)=0.2<2`

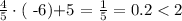
so, the point (-6,2) is in the yellow region