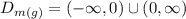Given the functions:
![\begin{gathered} g(x)=\frac{1}{\sqrt[]{x}} \\ m(x)=x^2-4 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/aj19bu1ge34bl3mquhiq1ybepbitewpig6.png)
I would like to find their domain as well and then complete the answers:
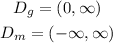
For the first question: g(x) / m(x)
![\begin{gathered} (g(x))/(m(x))=\frac{\frac{1}{\sqrt[]{x}}}{x^2-4}=\frac{1}{\sqrt[]{x}\cdot(x^2-4)}=\frac{1}{x-4\sqrt[]{x}} \\ x-4\sqrt[]{x}\\e0 \\ x\\e4\sqrt[]{x} \\ x^2\\e4x \\ x\\e4 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/cr65r95ollswjlp05bvghyl6ue58ppfzd9.png)
As we can see, the domain of this function cannot take negative values nor 4, 0. So, its domain is
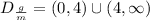
For the second domain g(m(x)), let's find out what is the function:
![\begin{gathered} g(m(x))=\frac{1}{\sqrt[]{x^2-4}} \\ \sqrt[]{x^2-4}>0 \\ x^2>4 \\ x>2 \\ x<-2 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/i3wulrm1fjkl3x7f9rrp6ulp5orjp956mp.png)
This means that x cannot be among the interval -2,2:
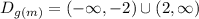
For the last domain m(g(x)) we perfome the same procedure:
![m(g(x))=(\frac{1}{\sqrt[]{x}})^2-4=(1)/(x)-4](https://img.qammunity.org/2023/formulas/mathematics/college/7q1lt1m4ms3dyowwczujbdqiobbltkw683.png)
For this domain it is obvious that x cannot take the zero value but anyone else.