Question

Find the formula for an exponential function that passes through the 2 points given

Answer 1

The form of the exponential function is

`f(x)=a(b)^x`

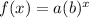
a is the initial value (value f(x) at x = 0)

b is the growth/decay factor

Since the function has points (0, 6) and (3, 48), then

Substitute x by 0 and f(x) by 6 to find the value of a

`\begin{gathered} x=0,f(x)=6 \\ 6=a(b)^0 \\ (b)^0=1 \\ 6=a(1) \\ 6=a \end{gathered}`

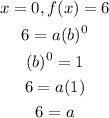
Substitute the value of a in the equation above

`f(x)=6(b)^x`

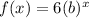
Now, we will use the 2nd point

Substitute x by 3 and f(x) by 48

`\begin{gathered} x=3,f(x)=48 \\ 48=6(b)^3 \end{gathered}`

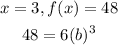
Divide both sides by 6

`\begin{gathered} (48)/(6)=(6(b)^3)/(6) \\ 8=b^3 \end{gathered}`

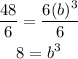
Since 8 = 2 x 2 x 2, then

`8=2^3`

Change 8 to 2^3

`2^3=b^3`

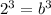
Since the powers are equal then the bases must be equal

`2=b`

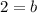
Substitute the value of b in the function

`f(x)=6(2)^x`

The answer is:

The formula of the exponential function is

`f(x)=6(2)^x`