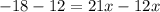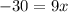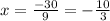We are supposed to solve the equation
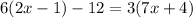
Here, we need to apply the distributive laws on both sides.
Comment: The distributive laws say that
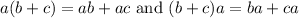
Using this comment we get
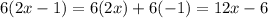
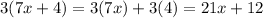
Then, our equation becomes
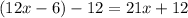
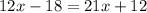
Now, let's apply the rule: terms with x on the right-hand side, and the rest on the left-hand side, to obtain