Question

Hello,Can you please help me with question # 25 in the picture?Thank you

Answer 1

To find the sum of an arithmetic sequence up to the nth term, we use the sum formula, which is

`S_n=n((a_1+a_n)/(2))`

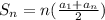
where a1 represents the first term, and an the nth term.

The general term of our sequence is

`a_n=3n+2`

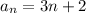
We want to sum up to the 16th term. Evaluanting n = 16 and n = 1 on this expression, we get the terms to plug in our formula

`\begin{gathered} a_1=3(1)+2=3+2=5 \\ a_(16)=3(16)+2=48+2=50 \end{gathered}`

Then, the sum is equal to

`\sum_{i\mathop{=}1}^(16)(3i+2)=16((50+5)/(2))=8\cdot55=440`

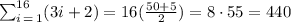
The result of this sum is 440.