Question

A decrease in smoking in the United States has resulted in lower death rates caused bylung cancer. The number of death rates per 100,000 people y can be expressed byy = - 26x2 - .55x + 91.81, where x represents the number of year after 2000.

Answer 1

Given the equation:

`y=-0.26x^2-0.55x+91.81`

Where x represents the number of years after 2000.

Let's solve for the following:

a.) Calculate the number of deaths per 100,000 for 2015 and 2017.

• For 2015, we have:

Number of years between 2015 and 2000 = 2015 - 2000 = 15

Substitute 15 for x and solve for y:

`\begin{gathered} y=-0.26(15)^2-0.55(15)+91.81 \\ \\ y=-0.26(225)-8.25+91.81 \\ \\ y=-58.5-8.25+91.81 \\ \\ y=25.06\approx25 \end{gathered}`

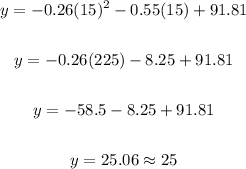
The number of deaths per 100,000 for 2015 is 25.

• For 2017:

Number of years between 2017 and 2000 = 2017 - 2000 = 17 years

Subustitute 17 for x and solve for y:

`\begin{gathered} y=-0.25(17)^2-0.55(17)+91.81 \\ \\ y=7.32\approx7 \end{gathered}`

The number of deaths oer 100,000 for 2017 is 7.

• b.) Let's solve for x when y = 50 using the quadratic formula.

Apply the quadratic formula:

`x=\frac{-b\pm\sqrt[]{(b^2-4ac)}}{2a}`

Now, subsitute 50 for y and equate to zero:

`50=-0.26x^2-0.55x+91.81`

Subtract 50 from both sides:

`\begin{gathered} 50-50=-0.26x^2-0.55x+91.81-50 \\ \\ 0=-0.26x^2-0.55+41.81 \\ \\ -0.26x^2-0.55+41.81=0 \end{gathered}`

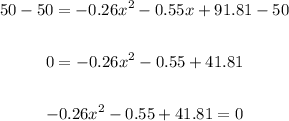
Apply the general quadractic equation to get the values of a, b and c:

`\begin{gathered} ax^2+bx+c=0 \\ \\ -0.26x^2-0.55+41.81=0 \end{gathered}`

Hence, we have:

a = -0.26

b = -0.55

c = 41.81

Thus, we have:

`\begin{gathered} x=\frac{-(-0.55)\pm\sqrt[]{-0.55^2-4(-0.26\ast41.81)}}{2(-0.26)} \\ \\ x=\frac{0.55\pm\sqrt[]{0.3025+43.4824}}{-0.52} \\ \\ x=(0.55\pm6.617)/(-0.52) \\ \\ x=-13.78,\text{ 11.}67 \end{gathered}`

Since the number of years cannot be a negative value, let's take the positive value 11.67

Therefore, the value of x is 11.67 when y = 50.