Question

the length of the rectangle is two feet less than 3 times the width.if the area is 65ft^2.find the dimension.

Answer 1

Given:

The area of the rectangle, A=65ft^2.

Let l be the length of the rectangle and w be the width of the rectangle.

It is given that the length of the rectangle is two feet less than 3 times the width.

Hence, the expression for the length of the rectangle is,

`l=3w-2\text{ ----(A)}`

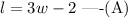
Now, the expression for the area of the rectangle can be written as,

`\begin{gathered} A=\text{length}* width \\ A=l* w \\ A=(3w-2)* w \\ A=3w^2-2w \end{gathered}`

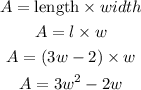
Since A=65ft^2, we get

`\begin{gathered} 65=3w^2-2w \\ 3w^2-2w-65=0\text{ ---(1)} \end{gathered}`

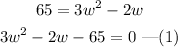
Equation (1) is similar to a quadratic equation given by,

`aw^2+bw+c=0\text{ ---(2)}`

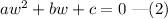
Comparing equations (1) and (2), we get a=3, b=-2 and c=-65.

Using discriminant method, the solution of equation (1) is,

`\begin{gathered} w=\frac{-b\pm\sqrt[]{^{}b^2-4ac}}{2a} \\ w=\frac{-(-2)\pm\sqrt[]{(-2)^2-4*3*(-65)}}{2*3} \\ w=\frac{2\pm\sqrt[]{4^{}+780}}{2*3} \\ w=\frac{2\pm\sqrt[]{784}}{6} \\ w=(2\pm28)/(6) \end{gathered}`

Since w cannot be negative, we consider only the positive value for w. Hence,

`\begin{gathered} w=(2+28)/(6) \\ w=(30)/(6) \\ w=5\text{ ft} \end{gathered}`

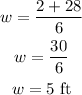
Now, put w=5 in equation (A) to obtain the value of l.

`\begin{gathered} l=3w-2 \\ =3*5-2 \\ =15-2 \\ =13ft \end{gathered}`

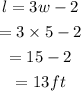
Therefore, the length of the rectangle is l=13 ft and the width is w=5 ft.