So we have a transformation that maps a triangle into another one. This is made by transforming the points X, Y and Z into X', Y' and Z'. In order to find out which of the four options is the correct one we must verify that points X, Y and Z actually transform into X', Y' and Z'.
We have:
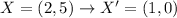
Let's see which of the four transformations do this. So for A:
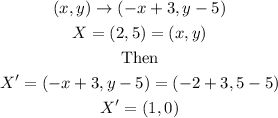
So transformation A is a possible answer, let's see the rest.
For C:
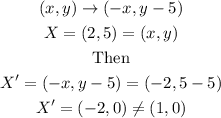
So the X' that we calculate with transformation C is different that the one we are looking for so we discard this option.
For option B we have:
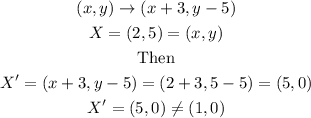
Like what happened with C, transformation B is discarded.
Let's see what happens with D:
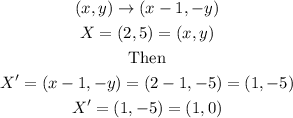
So D is also discarded. This would mean that A is the correct option but just in case, let's check if it tansform points Y=(0,2) and Z=(3,1) into Y'=(3,-3) and Z'=(0,-4):

So Y' and Z' are (3,-3) and (0,-4) which definetely means that option A is the correct one.