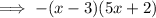Answer:

or
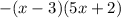
Explanation:
quadratic equation format:
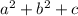
Therefore, for
 , a = -5, b = 13 and c = 6
, a = -5, b = 13 and c = 6
Multiply the coefficient of
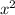 (
(
 ) by the constant term (
) by the constant term (
 )
)
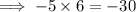
Find two numbers which have a product of -30 and a sum of
 (13)
(13)
Factors of 30: 1 and 30, 2 and 15, 3 and 10, 5 and 6
So -2 and 15 have a product of -30 and sum of 13.
Rewrite
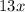 as
as
 and substitute into the equation:
and substitute into the equation:

Factorize the first two terms and the last two terms separately:
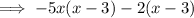
The bracket created should always be the same.
The two brackets have now been found. The first bracket is the common factor of (x - 3). The second bracket is the factorized terms outside of each bracket (-5x - 2).
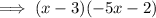
Additionally, we can write (-5x - 2) as -(5x + 2)