Question

Which is the equivalent of 6 14’ 48’’ written in decimal form Round to the nearest thousandth of a degree A. 6.145 B. 6.367 C. 6.247 D. 6.313

Answer 1

Explanation

First, we need to convert the 48'' into minutes. Using the conversion factor: 1' = 60'', we get:

`\begin{gathered} 48^(\prime)^(\prime)=48^(\prime)^(\prime)\cdot(1^(\prime))/(60^(\prime)^(\prime)) \\ 48^(\prime\prime)=(48)/(60)^(\prime) \\ 48^(\prime)^(\prime)=0.8^(\prime) \end{gathered}`

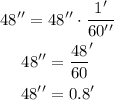
Then, 14 minutes and 48 seconds are equivalent to 14 + 0.8 = 14.8 minutes. To convert this amount of minutes into degrees we need to use the conversion factor 1° = 60', as follows:

In consequence, 6° 14’ 48’’ is equivalent to 6 + 0.247 = 6.247°