Question

Consider the following data. The expected value is -2.1.Find the variance, standard deviation, P(X ≥ -1), and P(X ≤ -3).

Answer 1

Given

The data,

To find:

The variance, standard deviation, P(X ≥ -1), and P(X ≤ -3).

Step-by-step explanation:

It is given that,

Then,

The variance is,

`\begin{gathered} Var[x]=(-4-(-2.1))^2*0.2+(-3-(-2.1))^2*0.3+(-2-(-2.1))^2 \\ *0.1+(-1-(-2.1))^2*0.2+(0-(-2.1))^2*0.2 \\ =(-4+2.1)^2*0.2+(-3+2.1)^2*0.3+(-2+2.1)^2*0.1+(-1+2.1)^2 \\ *0.2+(2.1)^2*0.2 \\ =3.61*0.2+0.81*0.3+0.01*0.1+1.21*0.2+4.41*0.2 \\ =0.722+0.243+0.001+0.242+0.882 \\ =2.09 \end{gathered}`

And the standard deviation is,

`\begin{gathered} SD=√(Var[x]) \\ =√(2.09) \\ =1.45 \end{gathered}`

Also,

`\begin{gathered} P\left(X≥-1\right)=P(X=-1)+P(X=0) \\ =0.2+0.2 \\ =0.4 \\ P\left(X≤-3\right)=P(-4)+P(-3) \\ =0.2+0.3 \\ =0.5 \end{gathered}`

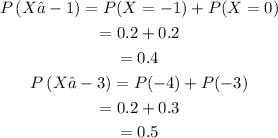
Hence, the answers are,

Variance is 2.09

Standard deviation is 1.45

P(X ≥ -1) is 0.4

P(X ≤ -3) is 0.5.