Question

Suppose you know students at school are, on average, 68 inches tall with a standard deviation of 4 inches. If you sample 36 students, what is the probability their average height is more than 70 inches?

Answer 1

0.135% or 0.00135

Explanation:

• The population mean height = 68 inches

,

• The population standard deviation = 4 inches

,

• Sample Size, n = 36

First, find the sample standard deviation:

`\sigma_x=(\sigma)/(√(n))=(4)/(√(36))=(4)/(6)=(2)/(3)`

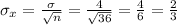
Next, for X=70, find the z-score:

`\begin{gathered} z-score=(X-\mu)/(\sigma_x) \\ z=(70-68)/(2\/3)=(2)/(2\/3)=3 \end{gathered}`

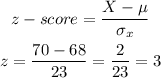
Since we are looking for the probability that their average height is more than 70 inches, we need to find:

• P(X>70)=P(z>3)

Using the z-score table:

`P(z>3)=0.0013499`

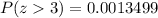
The probability that their average height is more than 70 inches is 0.135%.